Projets SCRATCH avancés

La série de projet suivante contient des projets SCRATCH de niveau “avancé”.

L’utilisation de Scratch est considérée comme acquise, tout comme les notions clés de l’algorithmique informatique.  Le raisonnement logique demandé pour concevoir ces programme est également plus ardu.  Ils abordent et utilisent :

la manipulation des variables à un niveau plus avancé,

les tests à un niveau plus complexe,

les listes (variables de type tableau).

Par ailleurs ils privilégient la programmation évènementielle par rapport à la programmation séquentielle.

Ils contiennent un générateur de labyrinthe, la programmation d’un jeu de plateforme, et la création d’une horloge à affichage binaire. De notre point de vue, les personnes qui ont atteint le niveau pour réaliser ces projets peuvent passer à un véritable langage de programmation. Ils demandent une logique qui n’est probablement accessible qu’en fin de cycle 4.

Chaque projet est décrit pas à pas, afin de pouvoir être utilisé en travaux dirigés. Ces projets  ne sont accessibles qu’aux comptes de type ‘Enseignant’. Chaque projet est disponible en téléchargement , entièrement commenté, avec une fiche PDF récapitulative et toutes ses ressources graphiques.

Info

SCRATCH 3 est sorti le 2 janvier 2019. Ces projets ont été fait avec SCRATCH 2, mais sont compatibles avec la dernière version de SCRATCH et les projets finis téléchargeables peuvent être ouverts et utilisés dans SCRATCH 3 sans problème. Nous préparons également des projets qui utilisent les nouveautés de cette dernière version!

Projets SCRATCH avancés

Générateur de labyrinthe

Description

Dans ce projet, nous allons voir comment programmer un générateur de labyrinthe avec SCRATCH. Générer des labyrinthes de manière dynamique sera, par exemple, particulièrement utile dans le développement de certains jeux car il permettra au programmeur de créer automatiquement différents tableaux, sans avoir à les concevoir lui-même ! Une fois encore, le code nous sert à faire accomplir à un ordinateur des tâches répétitives, longues et laborieuses à notre place !

D’un point de vue pédagogique ce projet demande une manipulation plus poussée des tableaux (ou listes), des boucles et des tests. Il s’agit également, ici, de réaliser un algorithme plus complexe que ceux qui ont pu être programmés dans les projets intermédiaires. Nous nous approchons plus d’une programmation « réelle ».

A notre sens, les élèves arrivant au terme de la programmation de ce type de projets sont très certainement prêts à aborder de « vrais » langages de programmation. (C’est d’ailleurs dans ce type de projet que les limites de Scratch commencent à se faire sentir)
Générer, ou modéliser, un labyrinthe.

Génération de labyrinthe – théorie

Il existe plusieurs algorithmes permettant de générer des labyrinthes parfaits (où chaque cellule est reliée à toutes les autres).

Dans ce projet, nous utiliserons la méthode la plus simple, qui fonctionne très bien pour les labyrinthes de taille modeste : une méthode d’exploration exhaustive. En effet, cette dernière ne demande pas d’opération ou de raisonnement complexe.

Pour comprendre comment générer un labyrinthe, revenons d’abord sur sa définition.

Info

Nous ne nous intéressons, ici, qu’à des labyrinthes de forme rectangulaire ou carrée, en 2 dimensions.

Un labyrinthe rectangulaire, ou carré, est un ensemble de cellules. Chaque cellule est composée de murs ouverts ou fermés. Et lorsqu’elles sont toutes reliées les unes aux autres de manière unique nous avons un labyrinthe parfait.

Voici un exemple de petit labyrinthe :

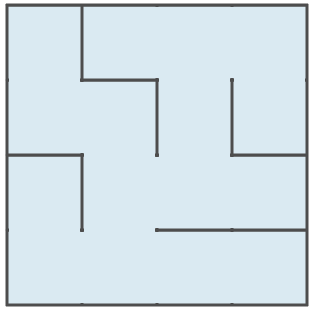
figure-1

Maintenant affichons ce même labyrinthe avec toutes ses cellules, que leurs murs respectifs soient ouverts ou non, nous obtenons ceci :

figure-2

Chaque cellule dispose de murs et chaque mur et soit ouvert, soit fermé.

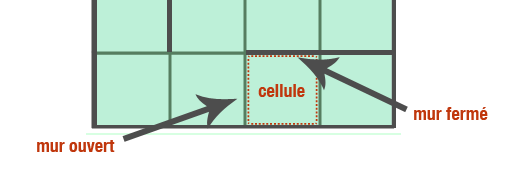
figure-3

Nous avons une grille de 4 cellules par 4 cellules, soit 16 cellules au total.

L’algorithme de génération

Voyons maintenant comment, avec une méthode d’exploration exhaustive d’une grille, nous allons pouvoir construire un labyrinthe à partir de cette dernière. Une fois le principe compris, nous n’aurons plus qu’à le programmer dans SCRATCH.

Les tâches que nous devons faire accomplir à notre programme seront donc les suivantes :

Dessiner une grille de m * n cellules (dans l’exemple en vidéo nous avons 4 x 4 ). Prendre une cellule de départ dans cette grille

Répéter de manière itérative les opérations suivantes :

marquer la cellule en cours comme étant visitée;

regarder si la cellule en cours dispose de cellules voisines qui n’ont pas été visitées;

Si elle en a :

Prendre une cellule au hasard;

Avancer jusqu’à cette cellule;

Considérer le mur entre la cellule d’où l’on vient et celle où l’on va comme ouvert.

Sinon

revenir sur nos pas jusqu’à que l’on soit dans une cellule qui dispose d’au moins une cellule voisine non visitée et recommencer.

Note

Pour qu’ils comprennent bien le processus, qui n’est finalement pas très complexe, il peut être intéressant de faire réaliser aux élèves un labyrinthe sur papier quadrillé. Au sein d’une même classe (et suivant le format de la grille) plusieurs labyrinthes différents pourront être produits. Une fois réalisé de cette manière, le passage au code devrait être plus aisé, car le raisonnement sera acquis.

Comment exprimer cet algorithme

Voyons comment il nous est possible de programmer ces différentes étapes.

Info

Ici nous décrirons les grands points de notre algorithme et les outils pour les implémenter dans SCRATCH. La réalisation complète du projet est quant à elle disponible dans la vidéo (voir la vidéo en fin de fiche).

La grille de départ

Nous ne nous en soucierons pas car ce n’est pas l’enjeu de ce projet. Nous vous donnons, avec le projet, un bloc appelé « dessiner la grille » qui fera cela automatiquement (importer une grille déjà dessinée dans SCRATCH cause plusieurs problèmes dus au manque de précision du logiciel au pixel près, ce qui, ici, serait cause d’erreur).

La cellule exploratrice

L’approche que nous allons avoir pour programmer cela dans SCRATCH va être de créer un lutin du format d’une cellule, posée dans la grille, et qui va explorer cette dernière suivant le principe décrit plus haut. Elle se déplacera jusqu’à avoir exploré toutes les possibilités. A chaque mouvement vers une cellule non visitée, elle ouvrira un mur dans la grille, c’est à dire que concrètement elle effacera un mur de la grille.

Tout le code que nous allons détailler maintenant sera donc placé dans ce lutin cellule exploratrice.

Les variables nécessaires

Comme vous le constatez en voyant la vidéo décrivant la méthode de génération, nous devons pouvoir stocker différents types de données :

la position de la cellule exploratrice, afin de gérer ses déplacements dans la grille;

la ou les directions possibles si des cellules non visitées sont à proximité;

les cellules visitées ou non dans la grille;

le trajet effectué au fur et à mesure afin de pouvoir revenir sur nos pas lorsque nous nous trouvons dans la situation où nous sommes dans une cellule qui ne dispose plus de cellules voisines non visitées.

Pour cela nous allons devoir utiliser différentes variables dont plusieurs de type liste (tableau dans SCRATCH)

Une grille et des listes

Ce dont nous avons réellement besoin, en premier lieu, est de pouvoir identifier chaque cellule. Pour cela, voyons comment nous pouvons tirer profit de notre structure en grille pour gérer nos données .

Nous pouvons identifier chaque cellule en utilisant sa position dans cette grille, suivant son indice de position horizontale et de position verticale. Nous nous trouvons sur un écran et plaçons notre grille en fonction de coordonnées x et y, notre premier élément sera donc 0,0 pour correspondre aux contraintes de positionnement :

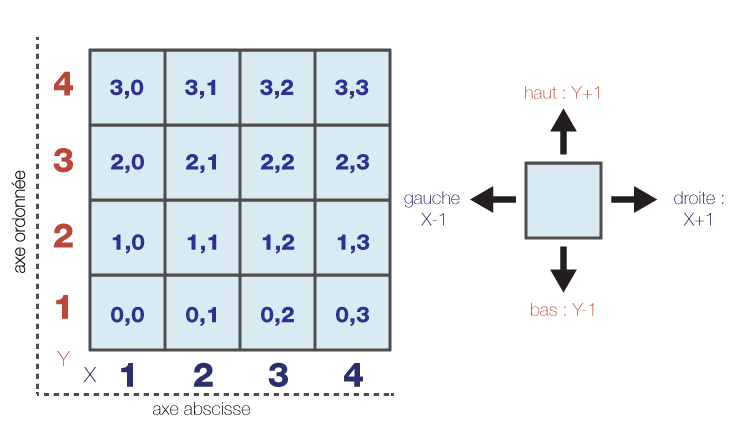
figure-4

La structure de la grille nous permet de déterminer la position de nos différentes cellules à l’écran, elle nous permet également de gérer celle de notre cellule “d’exploration”, ainsi que ses déplacements au cours de l’itération.

Prenons un exemple :

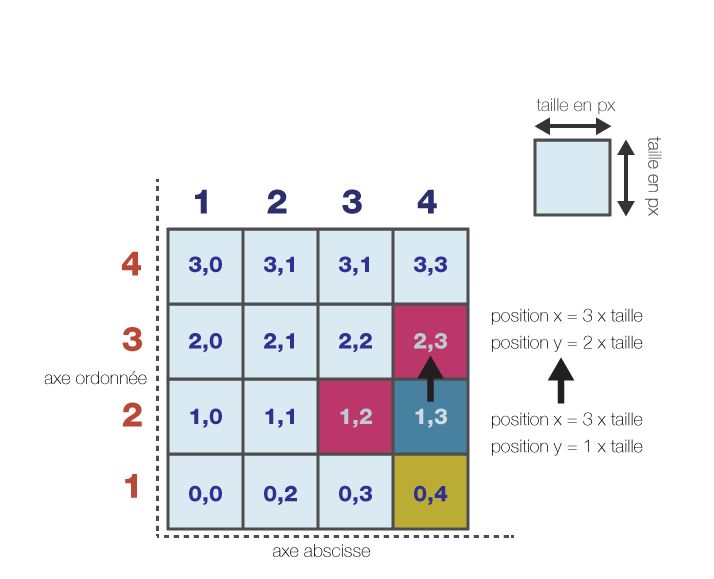
figure-5

La figure-5 représente notre grille, dans laquelle nous avons :

en 1,3 la cellule courante (ou cellule d’exploration);

en 0,4 une cellule déjà visitée;

et en 1,2 et 2,3 deux cellules voisines de notre cellule courante pouvant être potentiellement choisies pour la prochaine étape.

La position de chaque cellule à l’écran sera égale à:

son indice x multiplié par la taille de la cellule pour son abscisse;

son indice y multiplié par la taille de la cellule pour son ordonnée.

Admettons que nos cellules fassent 28 pixels de coté (c’est le cas dans le projet SCRATCH) :

la cellule 0,0 se trouvera donc à x=0 et y=0 sur le rapport orthonormé;

la cellule 0,1 se trouvera donc en x=0 et y=28;

la cellule 1,1 en x=28 et y=28, etc.

De la même manière, si nous souhaitons trouver la position sur l’écran de notre cellule exploratrice, elle sera de :

3 multiplié par la taille en pixels d’une cellule pour son abscisse;

1 multiplié par la taille en pixels d’une cellule pour son ordonnée.

Et si nous la déplaçons vers le haut, sa nouvelle position sera donc :

3 multiplié par la taille en pixels d’une cellule sur l’axe des abscisses;

2 multiplié par la taille en pixels d’une cellule sur l’axe des ordonnées (soit sa position initiale + 1).

Nous voyons donc qu’en parvenant à stocker les indices des positions verticales et horizontales de chaque cellule et en stockant la position de la cellule courante, nous pouvons effectuer toutes les opérations dont nous avons besoin pour faire fonctionner notre méthode d’exploration.

Quel type de variable utiliser

Rappel

Comme nous l’avons vu dans les ressources théoriques sur les tableaux, un tableau, ou liste dans SCRATCH, est une structure de données qui permet de stocker plusieurs éléments du même type. Ces éléments sont accessibles et identifiés par leur index de position dans ce tableau.

C’est exactement ce dont nous avons besoin et nous allons donc créer 4 listes.

Une liste pour gérer les cellules visitées

Nous stockerons ces cellules par la valeur de leurs positions horizontales et verticales dans la grille. Nous la nommerons cellules_visitees.

A chaque fois qu’une cellule aura été visitée, nous stockerons sa position dans la grille sous la forme d’une chaîne de caractères que nous créerons en concaténant : sa position x +’,’+ sa position y, et nous l’ajouterons à la liste cellules_visitees.

Par exemple, dans le cas de la figure-5, la liste contiendrait un seul élément : ‘0,4’.

Cette liste nous permettra de savoir quelles cellules n’ont pas été visitées et de voir dans quelle direction notre cellule exploratrice pourra se déplacer. En effet nous avons un nombre fini de cellules puisque nous sommes dans une grille. Logiquement, toute cellule ne se trouvant pas dans la liste des cellules visitées sera donc “non visitée”.

Les listes pour gérer la cellule exploratrice

Pour gérer la position de la cellule en cours, qui est en fait notre « cellule exploratrice », et son déplacement il nous faut créer 3 listes.

tableau_x

tableau_y

directions_possibles

Info

SCRATCH ne permet de créer des listes qu’à une seule dimension. Nous allons donc devoir créer plusieurs listes là où, dans un langage classique, nous n’utiliserions, par exemple, qu’un tableau à 2 dimensions (un tableau dont chaque élément contient lui-même un tableau)

stocker la position de la cellule exploratrice

A chacun de ses mouvements dans la grille, nous stockerons sa nouvelle position. Pour cela nous utiliserons 2 listes. En effet, lorsque nous devrons revenir sur nos pas, à certains moments de notre algorithme, nous n’aurons plus qu’à prendre les valeurs de ces 2 listes en partant de la dernière vers la première.

sa position x dans la grille dans une liste que nous appellerons tableau_x

sa position y dans la grille dans une liste que nous appellerons tableau_y

Les directions possibles que peut prendre la cellule exploratrice lors d’un déplacement

Lorsque nous trouvons des cellules non visitées adjacentes à notre cellule exploratrice, nous en prenons une au hasard et nous nous déplaçons vers elle. Pour cela, nous devrons la déplacer soit vers le haut, soit vers le bas, soit vers la gauche, soit vers la droite, suivant la position de chaque cellule voisine disponible. A chaque passage de notre itération nous allons donc définir les directions possibles, en fonction de chaque cellule disponible, et les stocker temporairement dans un tableau, ou liste, grâce à une suite de tests. Nous appellerons cette liste directions_possibles.

Si la cellule au dessus de la cellule courante n’est pas contenue dans le tableau des cellules visitées, alors on ajoute “haut” au tableau directions_possibles.

Si la cellule en dessous de la cellule courante n’est pas contenue dans le tableau des cellules visitées, alors on ajoute “bas” au tableau directions_possibles.

Nous ferons des tests pour les 4 directions possibles, puis nous en prendrons une au hasard. Ce tableau sera bien sûr vidé de ses valeurs à chaque nouvelle itération.

Par exemple, dans le cas de la figure-5, les deux directions temporairement stockées seront “haut” et “gauche” puisque les cellules disponibles se trouvent au dessus et à gauche de notre cellule exploratrice.

Les autres variables

Il nous faudra aussi stocker :

la taille en pixels d’une cellule puisque nous en avons besoin pour gérer les déplacements comme nous l’avons vu ci-dessus. Nous l’appellerons taille_cellule

La direction prise par notre cellule exploratrice lorsqu’une cellule non visitée aura été choisie : elle pourra avoir comme valeur haut, bas, droite ou gauche. Nous l’appellerons direction

La position x de la cellule exploratrice, pour gérer ses déplacements, que nous appellerons posx

La position y de la cellule exploratrice , pour gérer ses déplacements, que nous appellerons posy

Le pseudo code du lutin qui jouera le rôle de la cellule exploratrice

posx←0 // sa position x de départ posy←0 //sa position y de départ //nous commençons l’exploration dans le coin en bas à droite donc en 0,0 de notre grille //ce tableau contient notre position de départ comme cellule visitée Tableau cellules_visitees("0,0") //ce tableau contient la position x actuelle de notre cellule exploratrice Tableau tableau_x(posx) //ce tableau contient la position y actuelle de notre cellule exploratrice Tableau tableau_y(posy) //ce tableau contiendra toutes les directions possibles à chaque exploration Tableau directions_possibles() TantQue nombre d’éléments de Tableau cellules_visitees<largeur_grille*hauteur_grille //on vide le tableau contenant les directions possibles Tableau directions_possibles() Si posx>0 && Tableau cellules_visitées ne contient pas (posx-1)+","+posy Alors Ajouter "gauche" à Tableau directions_possibles Si posx<largeur_grille-1 && Tableau cellules_visitees ne contient pas (posx+1)+","+posy Alors Ajouter "droite" à Tableau directions_possibles Si posy>0 && Tableau cellules_visitees ne contient pas posx+","+(posy-1) Alors Ajouter "bas" à Tableau directions_possibles Si posx<hauteur_grille-1 && Tableau cellules_visitees ne contient pas (posy+1)+","+posy Alors Ajouter "haut" à Tableau directions_possibles Si longueur Tableau directions_possible>0 Alors direction←élément aléatoire de Tableau direction_possibles avancer d’une case et ouvrir mur dans : direction // nous avons créée un bloc spécifique dans Scratch, vous n’aurez pas à coder cette partie ajouter posx à Tableau tableau_x ajouter posy à Tableau tableau_y ajouter posx+","+posy à Tableau cellules_visitees Sinon //on prend la dernière position connue pour revenir d’un cran en arrière posx←dernier élément de Tableau tableau_x posy←dernier élément de Tableau tableau_y //on supprime la dernière position connue de nos 2 tableaux puisque nous revenons sur nos pas supprimer dernier élément de Tableau tableau_x supprimer dernier élément de Tableau tableau_y //on affecte la nouvelle position à notre lutin position x du lutin=taille_cellule*posx position y du lutin=taille_cellule*posy Fin Si Sinon Fin TantQue

La programmation de ce projet dans SCRATCH

.

.

Projets SCRATCH avancés

Horloge à affichage binaire

Description

Dans ce projet nous allons programmer une horloge à affichage binaire. C’est un gadget assez répandu chez les aficionados de programmation informatique (on peut acheter dans le commerce des montres ou des horloges ayant cet affichage). Ce projet associe l’utilisation de plusieurs concepts d’algorithmique : des boucles, des tests, le maniement des variables de type numérique et alphanumérique, et les listes. Il constitue donc un projet assez complet pour lequel il faut disposer déjà de certaines connaissances.

Comment lire une horloge à affichage binaire

Voyons tout d’abord comment lire ce type d’affichage!

L’affichage repose sur le système de numérotation appelé décimal codé binaire (DCB, binary coded decimal en anglais, BCD) dans lequel les nombres sont représentés par les chiffres décimaux les composant, et chacun codé sur quatre bits.
Ainsi pour coder un nombre, par exemple 12, il suffit de coder chacun des chiffres 1 et 2 ce qui nous donne 0001 et 0010.

Une horloge à affichage binaire prend 3 segments de temps : heure, minute et seconde (ou 2 sinon on choisit de ne pas afficher les secondes) et les représente en DBC, en affichant les 1 par une lampe allumée et les 0 par une lampe éteinte. Comme les heures, minutes ou seconde n’ont jamais plus que 6 dizaines (pour les mn et les secondes et 2 dizaine) pour les heures, l’affichage se fait en 2 colonnes, de chacune 4 lumières par segment de temps.

Chaque lumière représente une valeur de puissance de 2 (cf à ce sujet le cours sur le langage informatique et la conversion en binaire

Afin de lire l’heure, il suffit d’additionner les lampes allumées sur chaque colonne, et si aucune n’est allumée alors cela vaut pour “0”

Les étapes de la programmation de ce projet

Afin de programmer une horloge de ce type, nous devons effectuer les étapes suivantes :

obtenir les heures, min et secondes;

coder ces valeurs en DBC;

prendre les valeurs codées et assigner leur valeur à des lampes, qui, suivant qu’elles vaudront 0 ou 1, seront allumées ou éteintes.

Voyons chacune de ces étapes une à une.

Obtenir les heures minutes et secondes

Nous devons récupérer l’heure de l’ordinateur sur lequel tourne l’application. Il n’est pas question de code dans cet étape, chaque langage informatique dispose de fonctions prédéfinies à cet effet.
Dans SCRATCH, cela se fait très simplement grâce au bloc de type capteur (le petit menu déroulant nous permet de choisir la valeur temporelle que nous souhaitons récupérer).
Il nous suffira de stocker l’heure, dans une variable, idem pour les minute et les secondes, comme ceci :

Si vous placez ce groupe de bloc dans SCRATCH et que vous choisissez d’afficher les variables sur la scène, vous verrez l’heure s’afficher en temps réel.

Coder ces valeurs en DBC

Cette partie est la plus importante du programme. Nous la découperons en 2 étapes :

séparer les dizaines et les unités d’un nombre;

convertir un entier en binaire.

Une fois ses 2 aspects programmés, nous pourrons les appliquer à nos trois segments de temps. Et nous nous occuperons ensuite de l’affichage.
Ici, pour montrer le principe, nous nous occuperons des secondes. Le processus sera le même pour les minutes et les heures.
Voyons dans un premier temps comme séparer les dizaines et les unités.
Pour cela nous allons avoir recours à une opération très fréquemment utilisée en programmation : le modulo.

Le modulo

Rappel

Définition : le modulo est une opération arithmétique qui retourne le reste d’une division euclidienne. En informatique on le représente la plupart du temps par %.

Par exemple: 8%3 renverra 2.
8 / 3 = 3 * 2 + 2
Nous avons un quotient de 3 et bien un reste de 2.

Info

Le modulo peut s’avérer très utile et nous épargner des lignes de code de certains calculs. Par exemple dans le cas où nous souhaiterions déterminer si une valeur est paire ou impaire

Si x % 2 == 0 Alors Ecrire "x est pair" Sinon Ecrire "x est impair"

Pour récupérer le chiffre des unités d’un entier, le modulo va encore une fois nous servir, en effet en toute logique,, si nous avons un entier, entier%10 va nous donner le chiffre des unités.
Quant au nombre de dizaine d’un entier il nous suffit de prendre l’arrondi inférieur de notre entier / 10.

Voyons ce que cela nous donnerait en pseudo code:

nombre_entier←12 dizaine←0 unites←0 dizaine=arrondi inférieur de nombre_entier/10 unites=nombre_entier%10 Ecrire "nombre de dizaines : "+dizaine Ecrire "nombre d’unités : "+unites

Cet algorithme, une fois exécuté, affichera :
Nombre de dizaines : 1
Nombre d’unité : 2

Convertir un entier en binaire

Nous avons maintenant 2 entiers : l’un représentant les dizaines, l’autre les unités. Nous devons maintenant les coder au format DBC, c’est-à-dire les coder en binaire.
Pour cela, allons utiliser la méthode utilisant la division euclidienne par 2 :

on prend notre nombre en décimal;

on le divise par 2 et on note le reste de la division (cela sera soit un 1 soit un 0).;

on refait la même chose avec le quotient précédent, et on met de nouveau le reste de côté;

on réitère la division, et ce jusqu’à ce que le quotient soit égal 0.

Pour obtenir notre nombre en binaire, nous allons utiliser les restes que nous avons mis de côté : nous prenons le dernier reste non nul, puis nous remontons notre liste de reste en plaçant les plaçant successivement à sa gauche.
Prenons un exemple :

Pour programmer cet algorithme, nous voyons que nous devons réitérer la même opération un certain nombre de fois (dans la plupart des cas, c’est-à-dire dès que nous aurons un entier supérieur à 2). Nous allons donc utiliser une boucle.
Une fois encore, le modulo va nous éviter des lignes de code. En effet nous savons qu’il nous donne le reste d’une division euclidienne. Nous allons donc l’utiliser pour diviser par 2 notre entier.

Le point le plus épineux ici est de prendre le reste et de l’utiliser pour construire le nombre binaire, en effet cette opération ne relève plus du calcul mais de l’affichage. Cela signifie que nous allons devoir utiliser nos restes successifs pour construire une chaine de caractères en concaténant notre reste, en tant que caractère à chaque passage de la boucle.
Ici nous aurons donc le code suivant :

//notre entier de départ à convertir nombre←9 //attention cette variable est une variable alphanumérique vide pour commencer nombre_binaire←"" //Arbitrairement nous mettons cette variable reste à 0 pour commencer reste←0 TantQue nombre>0 Alors reste←nombre%2 //nous opérons maintenant une concaténation de chaîne nombre_binaire←reste+nombre_binaire Fin TantQue Ecrire nombre_binaire

L’algorithme suivant affichera: 1001.

Nous codons bien en binaire mais pas encore en DBC. En effet, ce dernier fait correspondre aux chiffres de 0 à 9 leur équivalent binaire sur 4 bit. Nous devons donc également traiter les cas où nous aurons un code binaire qui ne contiendra que 2 bit, par exemple 2 (11), voire même 0.

Pour cela nous allons faire une nouvelle manipulation de chaîne (notre variable contenant notre valeyr binaire est nous le rappelons maintenant de type alphanumérique) et procéder ainsi :
Si la longueur de la chaine contenant le nombre binaire est inférieure à 4, donc si elle contient moins de 4 caractères, nous ajoutons les 0 manquants jusqu’à ce que nous ayons une chaine de 4 caractères, et que nous ayons donc 4 bit.
En pseudo code cela pourra se traduire ainsi :

Nombre_binaire←11 Si longueur de nombre_binaire<4 TantQue longueur de nombre_binaire<4 Nombre_binaire←"0"+nombre_binaire Fin TantQue Fin Si

A l’issu de cet algorithme nombre_binaire aura pour valeur 0011 et pourra donc être affiché correctement par notre horloge.

Nous disposons maintenant de tous les éléments pour prendre nos heures, secondes et minutes et les coder en DBC.

L’affichage du format DBC

Eteint/Allumé

Revoyons le principe d’affichage de notre horloge avec un exemple :

Nous avons 8 lampes pour chaque segment de temps : 4 pour afficher les dizaines, 4 pour afficher les unités.
Prenons notre code DBC, chaque élément le constituant (0 ou 1) servira à allumer ou éteindre une lampe. Là encore, nous considèrerons notre DBC comme une chaine de caractère. Chaque lampe vérifiera si le caractère à laquelle elle est associée est égal à 0 ou 1, et s’allumera ou s’éteindra en fonction de cette valeur.

Le pseudo code d’une lampe sera donc relativement simple.

Si caractère 1 de nombre_binaire==1 Alors Lampe allumée Sinon Lampe éteinte Fin Si

Dans notre projet SCRATCH nous créerons un lutin par lampe.

Programmation dans SCRATCH

Voici maintenant comment réaliser ce projet dans SCRATCH.

Pour aller plus loin

Nous répétons, lors de ce programme, des codes identiques à plusieurs reprises ce qui n’est pas très optimisé. Il est possible de considérablement alléger ce code en créant un bloc personnalisé (donc une fonction) qui effectuera les opérations de codage en BDC. (le code du projet final à télécharger contient également cette fonction).

L’utilisation de lutins lampes individuels pourra également être optimisé en utilisant des clones.

.

.

.

Projets SCRATCH avancés

Jeu de plateforme nv 4 – partie 1

Description

Dans ce projet nous allons coder un jeu de plateforme complet. Nous allons réutiliser beaucoup de méthodes que nous avons vu dans d’autres projets ou ressources SCRATCH.

Dans ce jeu, le joueur doit aller délivrer la princesse retenue par un robot ! Pour cela, il doit monter jusqu’à elle en évitant les bombes que lui lance le robot. Le joueur dispose d’un nombre de vie limitée pour arriver à ses fins.

Ce projet est assez long et sera développé sur plusieurs séances. Il permet d’aborder les tests, les boucles, la manipulation de variables et l’utilisation d’expressions booléennes. Il permet, finalement, de programmer un vrai jeu, plus élaboré que dans les sections précédentes.

Dans ce jeu nous allons avoir plusieurs lutins qui auront tous un rôle dans le jeu :

le joueur;

la princesse;

le robot ennemi;

les bombes qui roulent;

les échelles;

les plateformes.

Dans cette première partie, nous allons nous occuper des mouvements du joueur sur la plateforme et les échelles. Notre joueur doit pouvoir effectuer les choses suivantes :

se déplacer vers la droite ou vers la gauche suivant si les touches droite ou gauche sont pressées;

monter lorsque qu’il est en contact avec une échelle et que la touche haut est pressée;

sauter pour éviter les bombes qui roulent et qui sont lancées par le robot ennemi (que nous ajouterons dans la seconde partie). Nous choisirons de déclencher un saut avec la barre espace.

Prenons ces étapes les unes après les autres.

Se déplacer sur des plateformes

Tout d’abord ajoutons l’arrière-plan , car il contiendra nos plateformes. Puis ajoutons notre lutin cody :

Déplacement du joueur

L’algorithme est simple (nous l’avons déjà vu plusieurs fois dans des projets plus courts, nous n’entrerons donc pas pas dans les détails) et le code utilisera les capteurs de touches directionnelles. A chaque touche pressée, flèche droite ou flèche gauche, nous incrémenterons ou décrémenterons la position x du lutin sur la scène.
Notre lutin cody, qui sera le joueur, aura 2 états : en train de marche ou en train de monter à l’échelle.
Nous allons donc créer une variable qui nous permettra de stocker cet état et de l’identifier lorsque cela sera nécessaire. Nous l’appellerons etat_joueur. Lorsque le joueur ira à droite ou à gauche, nous mettrons etat_joueur à marche.

Le code SCRATCH sera le suivant :

Note

Vous êtes évidemment libre de renommer les variables comme bon vous semble. Lorsque vous renommez une variable dans SCRATCH, il renomme automatiquement toutes ses occurrences présentes dans la fenêtre contenant le code.

Gestion des collisions

Notre joueur peut aller à droite et à gauche. Maintenant nous souhaitons qu’il se déplace suivant certaines contraintes : il ne peut marcher que s’il touche le sol. En effet, nous souhaitons donner l’illusion (et le jeu vidéo, tout comme le cinéma, est une succession d’illusions) que notre joueur est soumis à la gravité, pour autant nous n’allons pas programmer de lois gravitationnelles !

Tout d’abord, nous allons “capter” lorsqu’il touche le sol à l’aide d’un capteur prenant comme paramètre une couleur.Ensuite, nous allons définir une expression booléenne : touche la couleur du haut du sol, qui sera donc soit vraie, soit fausse. Lors d’une mise à jour constante (dans une boucle infinie), si elle est fausse, nous allons décrémenter la position y de notre lutin de 2. Ainsi, nous avons un semblant de gravité et, s’il ne touche pas le sol, notre joueur “tombe” jusqu’à ce qu’il le touche. Lorsqu’il rentrera en contact avec le sol, afin d’éviter un petit débordement visuel de 2 pixels, nous incrémenterons de 2 sa position y.

Monter à l’échelle

Notre joueur se déplace bien sur le sol. Maintenant faisons le monter à l’échelle. Pour cela nous avons séparé les échelles de l’arrière-plan. Créons un nouveau lutin qui contiendra toutes les échelles de notre jeu (l’image correspondante est contenue dans les ressources de ce projet), nommons le “echelle” et plaçons-le sur la scène. Visuellement, une fois sur la scène, ce lutin et l’arrière-plan semblent ne faire qu’un.

Nous allons poser un nouveau test et une nouvelle expression booléenne :

Si le joueur touche le lutin échelle et si la flèche directionnelle haute est pressée, alors on monte

Lorsque cette condition est remplie, nous changeons notre état du joueur à “monte”. Ainsi nous pourrons identifier à tout moment du jeu si le joueur marche, ou s’il monte (pour augmenter la difficulté du jeu nous ne laissons pas le joueur descendre).

Notre joueur marche et monte bien à l’échelle. Maintenant faisons le sauter.

Saut du joueur

Nous pourrions utiliser une méthode simple : lorsque l’on presse espace, on ajoute 15 à y, on attend une demi seconde (ou moins) et on revient à la position initiale. Cela fonctionne mais ça n’est pas très réaliste. Là encore, nous allons ajouter un peu de gravité au joueur et ainsi donner du réalisme au saut.

Pour cela, nous allons créer une variable, velocite_y à laquelle nous donnons une valeur de 5,5 (nous ne souhaitons pas qu’il saute trop haut). Nous allons procéder ainsi :

lorsque l’utilisateur appuiera sur la barre espace (ou n’importe quel évènement choisi pour déclencher le saut) nous allons ajouter la valeur de notre nouvelle variable à la position y du lutin joueur. Tout comme pour les déplacements, nous plaçons notre code dans une boucle infinie afin de gérer la mise à jour de ce qui se passe à l’écran;

à chaque passage de la boucle nous allons décrémenter notre variable de 0,6 (c’est la valeur de gravité que nous choisissons, suivant le format du jeu). En conséquence, notre joueur va monter jusqu’à un certain point, puis redescendre;

enfin, nous ajoutons un test de collision pour capter le moment où le joueur retouche le sol et le saut et remettre notre variable velocite_y à 0.

Si nous devions représenter schématiquement ce qui va se passer nous aurions à peu près ceci :

En langage SCRATCH nous aurons le script suivant (qui se trouvera donc dans une boucle infinie).

Comme nous ne souhaitons pas que notre joueur puisse sauter pendant qu’il est en train de monter sur une échelle, nous allons utiliser notre variable etat_joueur pour ne déclencher le script du saut que si elle est égal à “monte”. Nous allons donc placer le code ci-dessus dans un bloc de test.

Notre joueur peut maintenant avancer à droite et à gauche, monter aux échelles et sauter. Il nous reste à l’animer suivant ses différents états.

Animation du joueur

Lien

Là encore, l’animation est un point que nous avons déjà abordé. Nous ne rentrerons pas dans les détails d’une animation. Si vous souhaitez revoir le tutoriel vidéo sur l’animation d’un lutin, vous pouvez consulter la ressource “Changer de costume et animer un lutin” : cliquer ici

Pour animer notre joueur nous allons lui ajouter 6 costumes supplémentaires à l’aide de l’interface costume (ces costumes sont présents dans les ressources de ce projet). Les 5 premiers costumes seront utilisés pour animer le lutin lorsqu’il sera en état marche (nous avons stocké l’état du joueur dans la variable etat_joueur, et cela va nous servir dans cette série de blocs), et les 2 derniers pour animer le lutin sur une échelle lorsqu’il sera dans l’état monte.

Nous souhaitons aussi donner un costume au lutin lorsqu’il est à l’arrêt, pour cela nous mettons la variable etat_joueur à stop par défaut, c’est à dire au début de notre code gérant les mouvements. S’il est à l’arrêt sur une échelle nous basculerons sur un costume où on le voit en position de monter, sinon nous basculerons sur un costume où il est debout.

Notre lutin est maintenant capable de se déplacer, de sauter, de monter, et nous l’avons également animé en fonction de ces différentes actions.

Nous pouvons donc passer à la suite du programme : ajouter le robot ennemi et ses projectiles. C’est ce que nous verrons dans la fiche suivante.

.

Projets SCRATCH avancés

Jeu de plateforme nv 4 – partie 2

Description

Info

Cette fiche contient la suite du projet Jeu de plateforme nv 4 – partie 1.

Dans la fiche précédente nous avons programmé en grande partie notre lutin Cody, qui incarne le joueur. Il se déplace, saute et monte les aux échelles. Attaquons-nous maintenant à l’adversaire de ce jeu, dont le but est d’empêcher Cody d’atteindre la princesse en lui lançant des bombes qui exploseront à son contact !

Robotoc – le lutin qui incarne le méchant du jeu !

Son fonctionnement est finalement assez simple. Il est en haut de la plateforme et lance, à intervalle régulier, des bombes qui vont rouler au sol. Ses tâches sont donc les suivantes :

lancer une bombe,

attendre quelques secondes,

recommencer.

Pour coder cela nous allons ajouter 2 nouveaux lutins : le robot et la bombe.

Nous allons d’abord animer notre robot. A l’issue de chaque animation, il tirera un projectile : un lutin bombe.

Animation du robot

Nous importons les 5 costumes de notre robot (ils sont compris dans les ressources de ce projet). Tout d’abord, animons-le lorsqu’il tire. Pour une animation assez fluide nous espaçons chaque animation d’un dixième de seconde. A l’issue de notre animation, nous rebasculons sur le premier costume, celui où il est au repos, et attendons 3 secondes. En effet, c’est le temps que nous souhaitons entre chaque envoi de bombe.

Info

Pour une difficulté plus accrue, vous pouvez réduire le temps d’attente de 3 secondes entre chaque lancer (il faut cependant garder à l’esprit que SCRATCH supporte mal un trop grand nombre de clones d’un lutin présents à l’écran, et comme nous le verrons plus loin, nous allons utiliser des clones).

Le lancement de bombes

Afin qu’il puisse lancer une bombe, nous allons d’abord créer le lutin bombe.

Le principe sera le suivant : nous allons créer un clone de ce lutin à chaque fin d’animation de tir à l’aide du bloc de type contrôle créer un clone de. Nous allons créer un clone de notre bombe dès que l’animation de tir sera achevée, soit après le passage au costume robot_5 (ou du nom par lequel vous l’avez renommé).

Si nous testons notre code, nous voyons qu’à l’issue de l’animation de tir du robot, un nouveau lutin bombe apparait bien à l’écran. (Il apparait au même endroit que le premier lutin bombe).

Il répétera ces actions tant que Cody, donc le joueur, essayera de d’atteindre la princesse. En programmation SCRATCH nous écrirons cela grâce à une boucle jusqu’à et une expression booléenne composée :

Jusqu’à ce que le joueur ait gagné ou perdu, notre robot continue de lancer des bombes.

Nous allons utiliser deux nouvelles variables booléennes :

perdu, que nous mettrons à faux en début de partie (nous la placerons dans le lutin joueur, même si sa portée sera globale), et qui passera à vrai lorsque le joueur perdra la partie;

gagne, que nous mettrons à faux en début de partie (nous la placerons également dans le lutin joueur, même si sa portée sera globale) et que nous passerons à vrai lorsque / si le joueur atteindra la princesse.

A l’aide de ces deux variables nous allons pouvoir construire notre boucle, et répéter notre code de génération de bombe autant de fois que nécessaire. Nous placerons dans cette boucle tout le code vu précédemment.

Maintenant, programmons notre lutin bombe pour qu’il descende le long de la plateforme après sa création.

Le chemin d’une bombe

Examinons d’abord ce que nous souhaitons que notre lutin bombe exécute :

Une fois crée, la bombe roule au sol jusqu’en bas de la plateforme

Une fois arrivée en bas, si elle n’a pas rencontré d’obstacle (i.e. notre joueur) elle disparait

Si elle rencontre un obstacle (i.e. notre joueur) : le joueur meurt.

Prenons ces étapes une par une.

Etape 1 – rouler de haut en bas

Voici le trajet que nous souhaitons que chaque clone effectue :

Concrètement, cela signifie que notre lutin roulera, donc avancera, soit vers la droite, soit vers la gauche suivant la plateforme sur laquelle il se trouvera. Il existe plusieurs façons de gérer cela. Nous choisirons la suivante : en fonction de la position y de la bombe, nous allons pouvoir identifier sur quelle plateforme elle se trouve et, par conséquent, si elle doit rouler vers la droite ou vers la gauche.

Par exemple, si la position y de notre bombe est comprise entre -20 et -105, elle est forcément sur la deuxième plateforme en partant du bas. (cf les coordonnées sur la figure ci-dessus).

A partir des coordonnées de la bombe, des coordonnées y des plateformes, en procédant logiquement et par élimination nous allons pouvoir construire l’expression booléenne suivante :

Si la position y d’une bombe est supérieure à 60 || qu’elle est comprise entre -20 et -105 Alors elle avance vers la droite, donc nous incrémentons sa position x d’une valeur que nous choisirons Sinon elle avance vers la gauche , donc nous décrémentons sa position x d’une valeur que nous choisirons Fin Si

Dans SCRATCH, cela donnera ceci (nous choisirons 3 pixels comme valeur, mais si l’on souhaite aller plus vite on pourra évidement en prendre une plus élevée) :

Un peu de gravité

Par ailleurs, nous souhaitons que la bombe “roule sur le sol” et que lorsqu’elle n’est plus sur le sol, en fin de plateforme par exemple, elle “tombe”. Nous allons donc avoir recours à la même procédure que celle que nous avons effectuée pour le lutin du joueur. Nous allons tester si elle touche la couleur du sol grâce au bloc de type capteur approprié et, si ça n’est pas le cas, nous n’allons non plus incrémenter ou décrémenter la valeur de sa position x, mais décrémenter seulement celle de sa position y. Ainsi elle n’avancera plus et tombera jusqu’à ce qu’elle retouche à nouveau le sol.

Si le lutin touche le sol Alors Il avance sur le sol (dans une direction ou une autre) Sinon Il tombe Fin Si

Dans SCRATCH cela donnera :

Ce point étant programmé, passons à l’étape suivante.

Etape 2 – une fois son parcours réalisé le clone disparait

Une fois arrivé en bas, si le clone du lutin bombe n’a pas rencontré d’obstacle (i.e. notre joueur), nous devons faire disparaitre le clone. Pour cela, nous allons tout simplement détecter si notre lutin touche le bord, grâce au capteur approprié, et effectuer un test. Si notre clone touche le bord, on le fait disparaitre.

Passons maintenant à notre dernière étape

Etape 3 – Si une bombe rencontre un obstacle, c’est-à-dire notre joueur, le joueur meurt.

Nous allons maintenant créer une variable vivant, que nous mettrons à vrai en début de partie.

Nous allons effectuer le test suivant : si le clone touche le lutin Cody, alors le clone disparait et le lutin Cody meurt, on passe la variable vivant à faux. On envoie également un message que nous appellerons vie perdue. Ce message nous permettra d’écouter.

Si le clone bombe touche le lutin cody Alors Le clone disparait Le lutin cody meurt, On passe la variable vivant à faux. On envoie le message vie perdue. Fin Si

Attention

Maintenant que nous disposons d’une variable pour déterminer si notre lutin Cody est vivant ou non, nous devrons affiner certaines conditions que nous avons programmées dans la première partie de cette fiche. Notre lutin Cody ne pourra plus se déplacer s’il n’est pas vivant et nous ne l’animerons pas non plus dans ce cas. Nous revenons sur ce point dans la vidéo qui accompagne ce projet.

Gagné ou perdu

Il ne nous reste qu’à nous occuper de deux choses pour finir notre jeu : ses deux fins possibles. En effet, comme dans n’importe quel jeu, soit on perd, soit on gagne ! Nous avons déjà une variable booléenne gagne qui stocke l’état gagné, et une autre, nommée perdu qui stocke l’état perdu. En début de partie notre joueur n’a ni gagné, ni perdu. Et il ne finit une partie que si l’une de ces 2 variables prend la valeur vrai.

Posons les règles qui vont définir ses deux états.

Et nous allons définir :

que l’on gagne si le joueur arrive jusqu’à la princesse;

que l’on perd si notre joueur n’a plus de vie disponible;

que notre joueur perd une vie à chaque fois qu’il rentre en collision avec une bombe;

et que notre joueur aura trois vies au départ.

Vie et mort du joueur

Nous allons stocker le nombre de vies disponibles dans une nouvelle variable que nous appellerons vie. Nous allons lui affecter la valeur 3 au commencement du programme.

Maintenant que nous avons accès au nombre de vie disponible, nous allons pouvoir modifier cette valeur. Le seul moment où nous allons avoir à le faire sera lors d’une collision avec un des clones du lutin bombe. Nous allons donc poser un écouteur sur le message vie perdue que nous avons défini plus haut et retirer 1 à vie lorsque ce message sera reçu.

Il ne nous reste plus qu’à déterminer si la partie est finie ou pas, c’est-à-dire de vérifier si le joueur dispose encore de vies. Il nous reste à faire le test suivant :

Si le nombre de vie est inférieure à 0 Alors le joueur à perdu. Sinon on lui enlève une vie est on recommence. Fin Si

Gagner la partie

L’autre issue possible est de gagner la partie. Pour cela il faut atteindre la princesse.

Nous allons ajouter maintenant le dernier lutin dont nous avons besoin : celui de la princesse.

Très simplement, si le lutin Cody touche le lutin princesse, alors on affiche un message pour dire que l’on a gagné et on met la variable gagne à vrai (nous pourrions également stopper tous les scripts, mais si nous souhaitions, par exemple, ajouter de nouveaux niveaux à notre jeu, notre solution est meilleure). Nous allons donc avoir recourt encore une fois à un bloc de type capteur.

Notre programme est maintenant fini.

La vidéo du projet

Nous construisons ce projet pas à pas dans la vidéo suivante :

Pour aller plus loin

Ce jeu peut être amélioré de nombreuses façons. On pourra par exemple :

dessiner un ou plusieurs autres niveaux, avec des plateformes différentes et changer de niveau lorsque la princesse est atteinte. Pour cela, il faudra rajouter une variable qui stockera le niveau et réinitialisera les variables à chaque nouveau niveau;

ajouter des sons à chaque évènement spécifique, voire une musique de fond.

.

.